CLPS 0500 Perception and Mind, John Marks Guest Lecture Preparation (3)

Artist’s conception courtesy NASA JPL.

The above image is of a Voyager space probe. There is a fascinating connection between the Voyager program and Cultural Literacy in Music, and we will get to that soon.

But because my guest lectures will be Zoomed, I am concerned that if I sing or play musical examples, they might not come through well enough. Therefore, I want first to get some of the “Wires and Pliers” aspects of the physics of sound and music out of the way via uploads that you can look at and listen to. Here goes:

When I was a boy singer (I was a boy soprano, in fact) I had a music teacher who used to tell the story of a young musician or composer of the classical era (by which I mean circa 1775) who used to come home late after a night of carousing, and torment his musician or composer father (who was already in bed upstairs) by loudly playing all but the last note of a major-key octave scale.

Like so:

C-major scale in piano octaves, first seven notes:

There are two things going on.

First, each sonic event you hear is the result of two piano keys’ being pressed down at the same time. Those keys are one conventional Western “octave” apart on the piano keyboard. Musical pitches that are one octave apart have the same letter names. So the first sonic event you hear, a two-note “chord,” is the note “C” below Middle C being played at the same time as the note Middle C. And so on.

Secondly, the sequence of seven two-note chords you hear goes through the differently-named pitches of the conventional Western C-major scale (C-D-E-F-G-A-B); but the sequence does not include the final two-note chord on “C” to complete the octave.That’s because that long-dead young composer or musician used to torment his father that way.

You may or may not know the memory-aid song from The Sound of Music, “Doe, a Deer, a Female Deer,” which makes use of the fact that the note name “Do” has the same sound as the word “Doe.” The Do-Re-Mi system, at least in the US, is a “moveable” system in which the first note of the scale, regardless of its pitch name, gets called “Do.” Therefore, as the song goes, the final note of the scale “brings us back to ‘Do’.”

I think that it is fair to say that most of the music of Western Civilization—songs, hymns, and classical music—starts and ends with the same pitch or note (or, in the case of classical music, is built up of parts or movements that start and end at the same pitch or note). The conventional wisdom is that music’s having a “tonal center” or a “key note” is important in music (meaning that people want it and expect it), and that when a piece of music is tonal (in a key), people derive a sense of completion or fulfillment when the piece ends in the “tonic” note of the home key. And the point of my music teacher’s little story above is that a trained musician (which the father supposedly was), especially in the classical era, would be driven nuts by an incomplete scale that did not achieve closure.

So then, the father would absolutely feel that he had to get out of bed, come downstairs to the piano, and play the final chord. (I can’t remember who the kid was; perhaps it was supposedly Mozart.)

Final “Do” of C-major scale:

Pop Quiz:

Was the father’s need to play the concluding “Do”:

(a) baked in the loaf of physical reality;
(b) hard-wired into his brain;
(c) culturally determined; or
(d) a certain amount of all of the above.

HINT: The correct answer is (d).

Here’s an audio spectrum of the first “C” two-note chord:

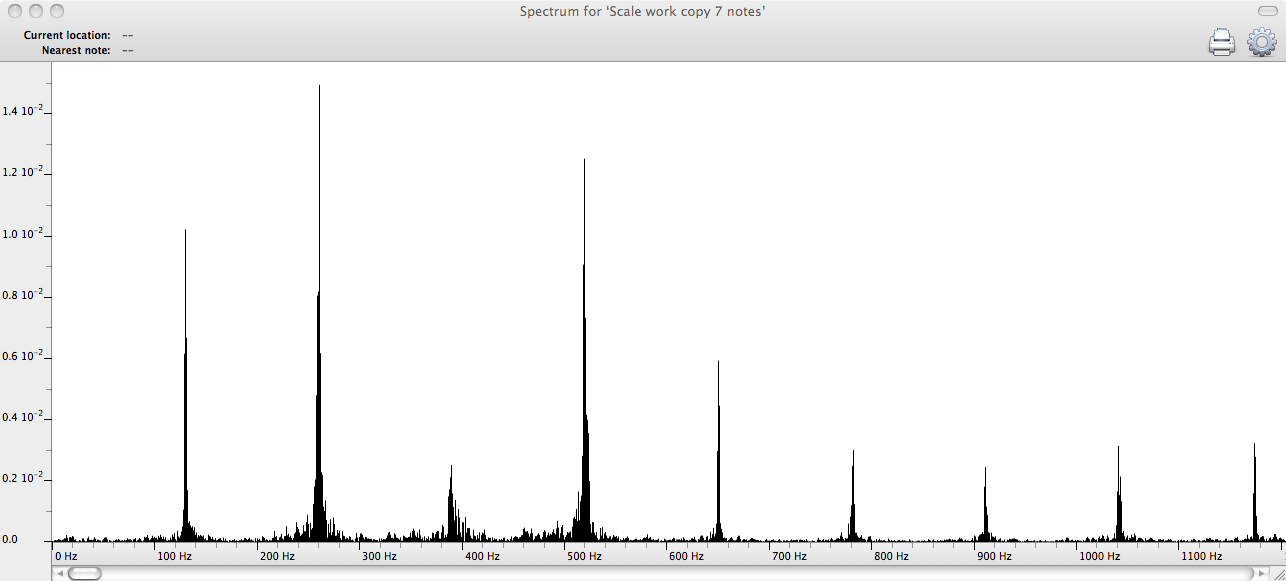
The spike on the far left is the C below middle C, circa 130.8 Hz. The next one is Middle C at circa 261.6 Hz. There’s something interesting going on there. This passage was played for me by a professional musician who in his youth was a protégé of Leonard Bernstein’s. I asked him to play very simply and straightforwardly, and he did.

But the spike at Middle C is higher than the one for the note the octave below, which means that that note was louder. Did he press harder on one note than the other? No. What is happening is that the acoustical energy (airborne vibrations, as well as vibrations carried by the piano’s frame and case) from the lower note reinforced via “additive interference” the upper note.

Even more interesting is the small spike to the right. That frequency is circa 392 Hz, which is the frequency for G above middle C. Problem is, that note was not played! What is happening is that, unlike an electronic sine-wave generator or a tuning fork, a piano string does not vibrate only at its fundamental frequency. The piano string also generates overtones or harmonics, which was explored by the Pythagoras (sixth century BCE).

A string will vibrate in its full length at its fundamental frequency (a ratio of 1:1), but also (with less energy) at integer fractions such as 1/2 and 1/3. When instead of vibrating along its entire length, a string vibrates in two sections, its frequency is twice as high—which is also the definition of the octave relationship. So, here, the lower string is vibrating strongly at circa 130.8 Hz but also weakly at 261.6 Hz, and that adds to the strength of the upper note.

But both of the played strings are also vibrating in thirds, which instead of the frequency ratio 2:1 gives us the frequency ratio 3:2, or, 150%. Now, the frequency of the small spike to the right, G at 392 Hz, a note the pianist did not press down the key for, happens to be 150% of Middle C at 261.6 and also 300% of the lower C at 130.8 Hz. The musical relationship between C and G is that of a “fifth.”

That is potentially misleading, for two reasons. First, it is not a question of something’s being one-fifth of something else, as is the case of a bottle of vodka’s being one-fifth of a gallon. This figure of speech only means that in a conventional Western scale, when you start with C and include it in the counting, G is the fifth note. The second pitfall is that to call G the fifth note implies that there are only three notes between C and G, whereas there are at least 6: C sharp, D, D sharp, E, F, and F sharp.

Moving to the right on the spectrum, the large spike circa 523.3 Hz, again, a note that the pianist did not play, is C, two octaves above the lower C. The remaining small spikes represent the pitches of other complex overtones or harmonics.

So, certain pitch relationships are indeed NOT culturally determined, but rather baked into the loaf of the properties of physical objects or materials like strings or columns of air in a pipe. Which is why Pop Quiz answer (a) is right, but not the only one that is right.

One of the big concepts I want to get across to you is that while some aspects of music perception (and reception) are culturally determined, many aspects of music perception are, to use my favorite turn of phrase, “non-negotiable,” in that they are based on the physical properties of material objects and/or the ways the ear/brain system is structured and works.

If you suspend a wire in tension between two hard points (think of a string on an electric guitar), it will vibrate at a certain frequency. Shorten the string by 50%, and it will vibrate twice as fast, and the sound it makes will sound to humans, at the same time different from, yet in some way identical to, the earlier sound.

Here’s a sine wave with a 110 Hz A in the left channel and a 55 Hz A in the right channel; first a few seconds of audio, and then a waveform graph.

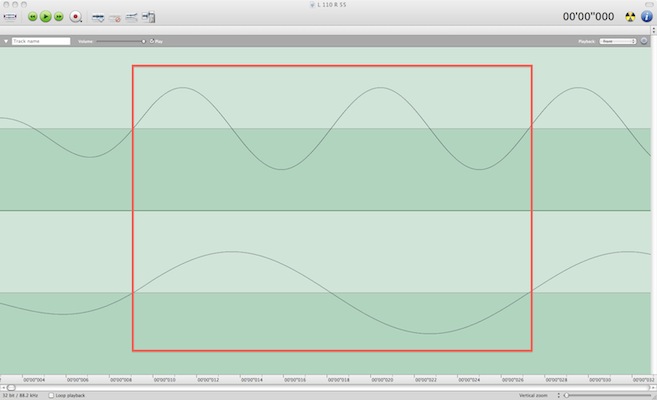
The “non-negotiable” reason that the lower-frequency A at 55 Hz and the higher-frequency A at 110 Hz sound “both the same yet differently” is that the higher-frequency tone has a shorter wavelength that is exactly half that of the higher tone. Therefore, two cycles of the higher tone nest perfectly inside the longer wavelength of one cycle of the lower tone. Regardless whether you find yourself in Iowa, or in Istanbul.

When the cycles nest perfectly, the zero-axis crossings of one cycle of the lower tone are identical in time with the “outer” (first and last) zero-axis crossings of two cycles of the higher note. So there is no conflict when our ear-brain system relies upon the zero-axis crossings, which are the zero-motion points in time of the air molecules (as the sine wave, and therefore the air pressure, changes phase from positive to negative), as the time clock to determine frequency or pitch.

Much the same thing allows our ear-brain system to hear the musical interval of the fifth as more consonant than dissonant, because the odd-order harmonics of the higher note correspond to the even-order harmonics of the lower note; the zero-axis crossings correspond as much as they miss each other. Which is why Pop Quiz answer (b) is also right.

But one would be simply wrong, were one then to conclude that an overwhelming preference for tonality, for consonant intervals, for the resolution of harmonic tension, and other hallmarks of Western music do not evidence some degree of cultural determination, that they are just they way physics works and the way our brains are wired.

As my next (and final) “message in a bottle” to you will show, there is much diversity in human music, and some cultures have solved the many problems and challenges of the Western system of scales by embracing dissonance, Indonesian gamelan being a prime example.

I will leave the last word tonight to a Black-Capped Chickadee bird, singing call-and-response with a neighbor. Singing down from A to G, a whole step apart, in the 7th octave.

Poecile atricapillus – Black-capped Chickadee.mp3

 

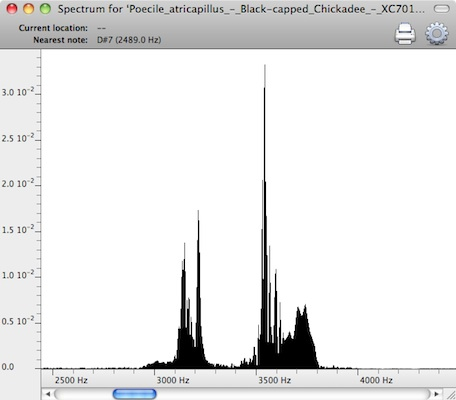
Just about perfectly in tune.

# # #